CUDA核函数详解（一）

笔者在本科阶段实现了一个Edge-Compute-Engine，但是实现的比较粗糙和简单，计划通过cuda进行矩阵方向的重构和加速，顺便记录一些内容。

在 GPU 编程中，CUDA（Compute Unified Device Architecture）使得并行计算得以高效实现。在 CUDA 中，矩阵加法是第一个入门操作，因其简单且能展示 CUDA 中线程并行化的核心概念。本文将从最底层的原理开始，实现矩阵加法的 CUDA 核函数，并深入讨论其实现背后的一些信息。

1. 什么是矩阵加法？

矩阵加法是线性代数中的一种基本运算，定义为两个矩阵对应元素的逐一相加。对于给定的矩阵 A 和 B，矩阵 C 的每个元素

\begin{matrix} (1) & C [i] [j] \end{matrix}

由

\begin{matrix} (2) & C [i] [j] = A [i] [j] + B [i] [j] \end{matrix}

给出。

我们要做的，就是把这个运算搬到 GPU 上，并利用并行计算的优势加速这个操作。

2. （必知必会）CUDA 基础

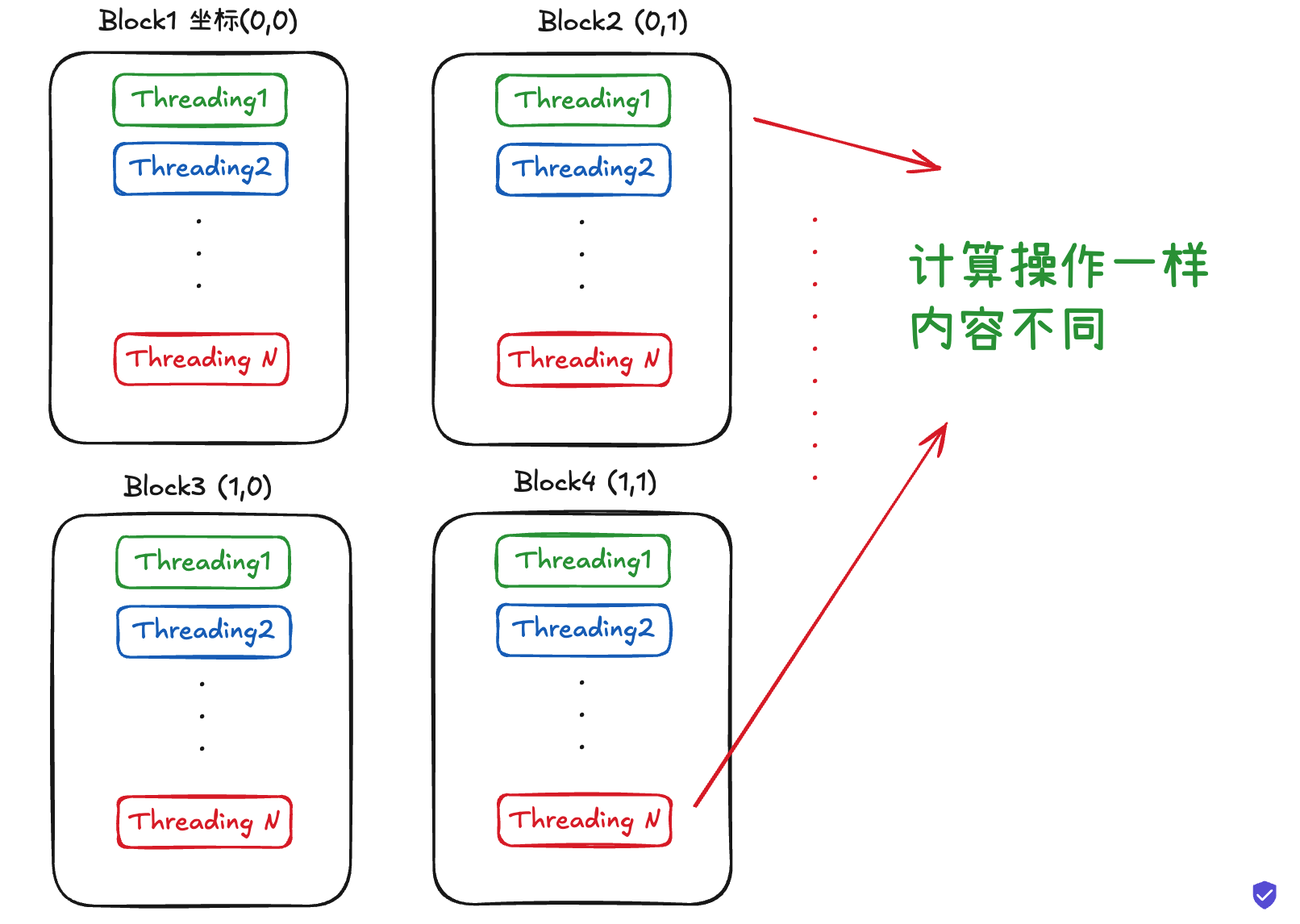
在 CUDA 中，计算任务被分配给大量并行线程来完成。每个线程都执行同样的操作，但作用于不同的数据片段。为了实现这一目标，CUDA 使用网格（grid）和块（block）的结构。

• 线程块（Block）：是一个线程的集合，所有线程在同一个块内可以共享内存。

• 网格（Grid）：由多个线程块组成。

每个线程在自己的计算中有一个唯一的 ID，这些 ID 用于标识它在线程块和网格中的位置。

简单画了一个图：

3. CUDA 核函数解析

接下来，我们来看一个实现矩阵加法的 CUDA 核函数：


xxxxxxxxxx
__global__ void matrixAddKernel(const float* A, const float* B, float* C, int rows, int cols) {
    int idx = blockIdx.x * blockDim.x + threadIdx.x;
    int idy = blockIdx.y * blockDim.y + threadIdx.y;
    
    if (idx < rows && idy < cols) {
        int linear_idx = idx * cols + idy;
        C[linear_idx] = A[linear_idx] + B[linear_idx];
    }
}

3.1 输入参数

• A 和 B：矩阵 A 和矩阵 B 的指针，它们存储在 GPU 上的全局内存中。

• C：矩阵 C 是最终结果矩阵，也会存储在 GPU 上的全局内存中。

• rows 和 cols：矩阵的行数和列数。

3.2 核心逻辑

让我们逐步解析每一行代码的实现细节：

3.2.1 计算线程的索引

上图为例：

块内线程可以有xyz三维坐标：

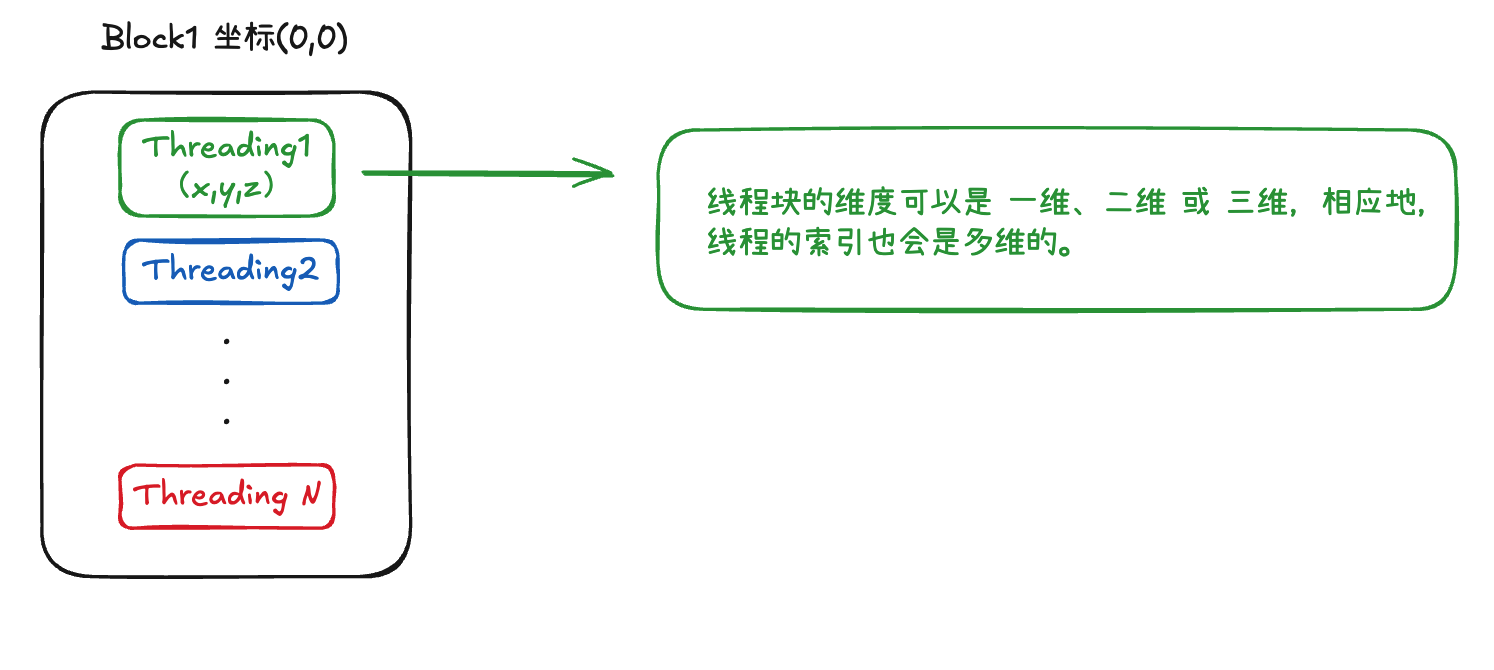在我们的例子里面：


xxxxxxxxxx
int idx = blockIdx.x * blockDim.x + threadIdx.x;
int idy = blockIdx.y * blockDim.y + threadIdx.y;

• blockIdx.x 和 blockIdx.y 分别表示线程块在 x 和 y 方向上的索引。

• blockDim.x 和 blockDim.y 表示每个线程块在 x 和 y 方向上包含的线程数。

• threadIdx.x 和 threadIdx.y 分别表示线程在其所属块内的 x 和 y 方向上的索引。

通过这几个值的组合，我们能够计算出当前线程在矩阵中的横向索引 idx 和纵向索引 idy。

3.2.2 边界检查


xxxxxxxxxx
if (idx < rows && idy < cols) {

CUDA 中的线程会按照网格结构启动，某些线程可能会对应矩阵外部的无效位置，因此在执行矩阵加法之前，我们需要检查当前线程的索引是否在矩阵的有效范围内。如果超出范围，线程将不执行任何操作，从而避免越界访问。

3.2.3 计算线性索引


xxxxxxxxxx
int linear_idx = idx * cols + idy;

由于矩阵在内存中通常是以行主序（row-major order）存储的，因此我们需要将二维的 idx 和 idy 转换为线性的一维索引 linear_idx。这个转换的公式是：

\begin{matrix} (3) & l i n e a r_i d x = i d x \times c o l s + i d y \end{matrix}

这样，我们可以通过 linear_idx 直接访问矩阵中的元素。

3.2.4 执行加法操作


xxxxxxxxxx
C[linear_idx] = A[linear_idx] + B[linear_idx];

这里，我们将矩阵 A 和 B 对应位置的元素相加，结果存储到矩阵 C 的对应位置。这一操作是并行执行的，每个线程负责处理一个元素的加法。

linear_idx = idx * cols + idy：这是将二维的 (idx, idy) 坐标转换为 一维索引。在矩阵的存储方式中，通常是 按行主序（Row-major order） 存储的，因此，二维坐标可以转换为线性索引（展平操作）。这样，每个线程就能计算出它应该处理的矩阵位置。

• 矩阵加法： C[linear_idx] = A[linear_idx] + B[linear_idx] 这个操作就是每个线程执行的任务，直接将 A 和 B 对应位置的元素相加，并存入 C 的对应位置。

而后就直接并行化，无需显式循环。

3.3 测试

3.3.1 第一步：定义Matrix


xxxxxxxxxx
struct Matrix_CU {
    int row;
    int col;
    float* data;

    Matrix_CU(int r, int c) : row(r), col(c) {
        data = new float[r * c]();
    }

    Matrix_CU(const Matrix_CU& other) : row(other.row), col(other.col) {
        data = new float[row * col];
        std::memcpy(data, other.data, row * col * sizeof(float));
    }


    Matrix_CU& operator=(const Matrix_CU& other) {
        if (this != &other) {
            delete[] data;
            row = other.row;
            col = other.col;
            data = new float[row * col];
            std::memcpy(data, other.data, row * col * sizeof(float));
        }
        return *this;
    }
    ~Matrix_CU() {
        delete[] data;
    }

    void randomInit() {
        for (int i = 0; i < row * col; ++i) {
            data[i] = static_cast<float>(rand()) / RAND_MAX;
        }
    }

    void printFirstElement() const {
        std::cout << "First element: " << data[0] << std::endl;
    }
    void printSubMatrix(int numRows, int numCols) const {
    for (int i = 0; i < numRows; ++i) {
        for (int j = 0; j < numCols; ++j) {
            std::cout << data[i * col + j] << " ";
        }
        std::cout << std::endl;
        }
    }
    
};

这里的定义来自我自己实现的https://github.com/AllenZYJ/Edge-Computing-Engine#：

• row 和 col 分别表示矩阵的行数和列数。

• data 是一个指向 float 类型的指针，用来存储矩阵的数据。矩阵的数据是按行主序（row-major order）存储的，即矩阵的每一行按顺序存储在内存中。

这里的构造函数接受行数 r 和列数 c 作为参数，并通过 new 关键字在堆上分配一个大小为 r * c 的 float 数组来存储矩阵的数据。括号 () 表示将数据初始化为 0。

接下来是拷贝构造函数：


xxxxxxxxxx
Matrix_CU(const Matrix_CU& other) : row(other.row), col(other.col) {
    data = new float[row * col];  // 分配新的内存
    std::memcpy(data, other.data, row * col * sizeof(float));  // 复制数据
}

拷贝赋值函数：


xxxxxxxxxx
Matrix_CU& operator=(const Matrix_CU& other) {
    if (this != &other) {  // 防止自赋值
        delete[] data;  // 释放当前对象的内存
        row = other.row;
        col = other.col;
        data = new float[row * col];  // 重新分配内存
        std::memcpy(data, other.data, row * col * sizeof(float));  // 复制数据
    }
    return *this;
}

它们负责对象的复制过程。它们的主要作用是在对象的创建和赋值时，确保正确的内存管理，避免潜在的错误和资源泄漏。

在大规模计算，尤其是涉及大量数据和高效内存管理的计算任务中，如果没有显式定义拷贝构造函数和拷贝赋值运算符，C++ 会使用默认的拷贝构造函数和赋值运算符，通常会进行浅拷贝（shallow copy）。浅拷贝只会复制对象的成员变量（例如指针），而不会复制指针指向的内存区域。这意味着两个对象会共享同一块内存。

3.3.2 实现核函数调用

matrixAddCUDA 函数的作用是使用 CUDA 进行矩阵加法计算。它接受三个 Matrix_CU 类型的参数：A、B 和 C，分别表示输入的两个矩阵和输出的矩阵。具体步骤如下：


xxxxxxxxxx
void matrixAddCUDA(const Matrix_CU& A, const Matrix_CU& B, Matrix_CU& C) {
    assert(A.row == B.row && A.col == B.col);
    assert(A.row == C.row && A.col == C.col);
    
    const int rows = A.row;
    const int cols = A.col;
    size_t size = rows * cols * sizeof(float);
    
    float *d_A, *d_B, *d_C;
    

    CHECK_CUDA_ERROR(cudaMalloc(&d_A, size));
    CHECK_CUDA_ERROR(cudaMalloc(&d_B, size));
    CHECK_CUDA_ERROR(cudaMalloc(&d_C, size));


    CHECK_CUDA_ERROR(cudaMemcpy(d_A, A.data, size, cudaMemcpyHostToDevice));
    CHECK_CUDA_ERROR(cudaMemcpy(d_B, B.data, size, cudaMemcpyHostToDevice));


    dim3 blockSize(16, 16); // 256 threads per block
    dim3 gridSize((cols + blockSize.x - 1) / blockSize.x,
                 (rows + blockSize.y - 1) / blockSize.y);
    auto start = std::chrono::high_resolution_clock::now();

    matrixAddKernel<<<gridSize, blockSize>>>(d_A, d_B, d_C, rows, cols);
    auto end = std::chrono::high_resolution_clock::now();
    std::chrono::duration<double> elapsed = end - start;
    std::cout << "GPU执行时间: " << elapsed.count() * 1000 << " ms\n";
    CHECK_CUDA_ERROR(cudaGetLastError());
    

    CHECK_CUDA_ERROR(cudaMemcpy(C.data, d_C, size, cudaMemcpyDeviceToHost));


    CHECK_CUDA_ERROR(cudaFree(d_A));
    CHECK_CUDA_ERROR(cudaFree(d_B));
    CHECK_CUDA_ERROR(cudaFree(d_C));
}

接下来，调用这个函数


xxxxxxxxxx
const int rows = 10240;
const int cols = 10240;    
Matrix_CU A(rows, cols);
Matrix_CU B(rows, cols);
Matrix_CU C_gpu(rows, cols);  // GPU结果矩阵
matrixAddCUDA(A, B, C_gpu);

编译执行：


xxxxxxxxxx
nvcc -arch=sm_80 -I/usr/local/cuda/include -L/usr/local/cuda/lib64 cuda_mat/matrix_cudadef.cu -o conv_test && ./conv_test

结果：


xxxxxxxxxx
使用GPU: NVIDIA GeForce RTX 4090
测试矩阵大小: 10240x10240
矩阵A: First element: 0.840188
矩阵B: First element: 0.301959
CPU版本:
CPU执行时间: 419.75 ms
CPU结果: First element: 1.14215（第一个元素求和结果）
GPU版本:
GPU执行时间: 0.137581 ms
GPU结果: First element: 1.14215（第一个元素求和结果）
标准差:0.612201最大值: 1.99991
最小值: 0.000145095
平均值: 0.32
和: 3.35544e+07
标准差: 0.612201

以上实验完整代码：

Matrix_cuda_def