RoPE旋转位置编码理解
1、概述
在 Transformer 中,注意力本身是位置无关的。
RoPE(Rotary Position Embedding)通过一种非常巧妙的方式,把位置信息耦合到注意力结果中,并且让注意力天然感知相对位置。
把向量的每一对维度当作二维平面,在不同位置上按不同角度旋转。
向量本身不变长
旋转角度由位置决定
点积结果天然会包含相对位置信息,而与绝对位置无关
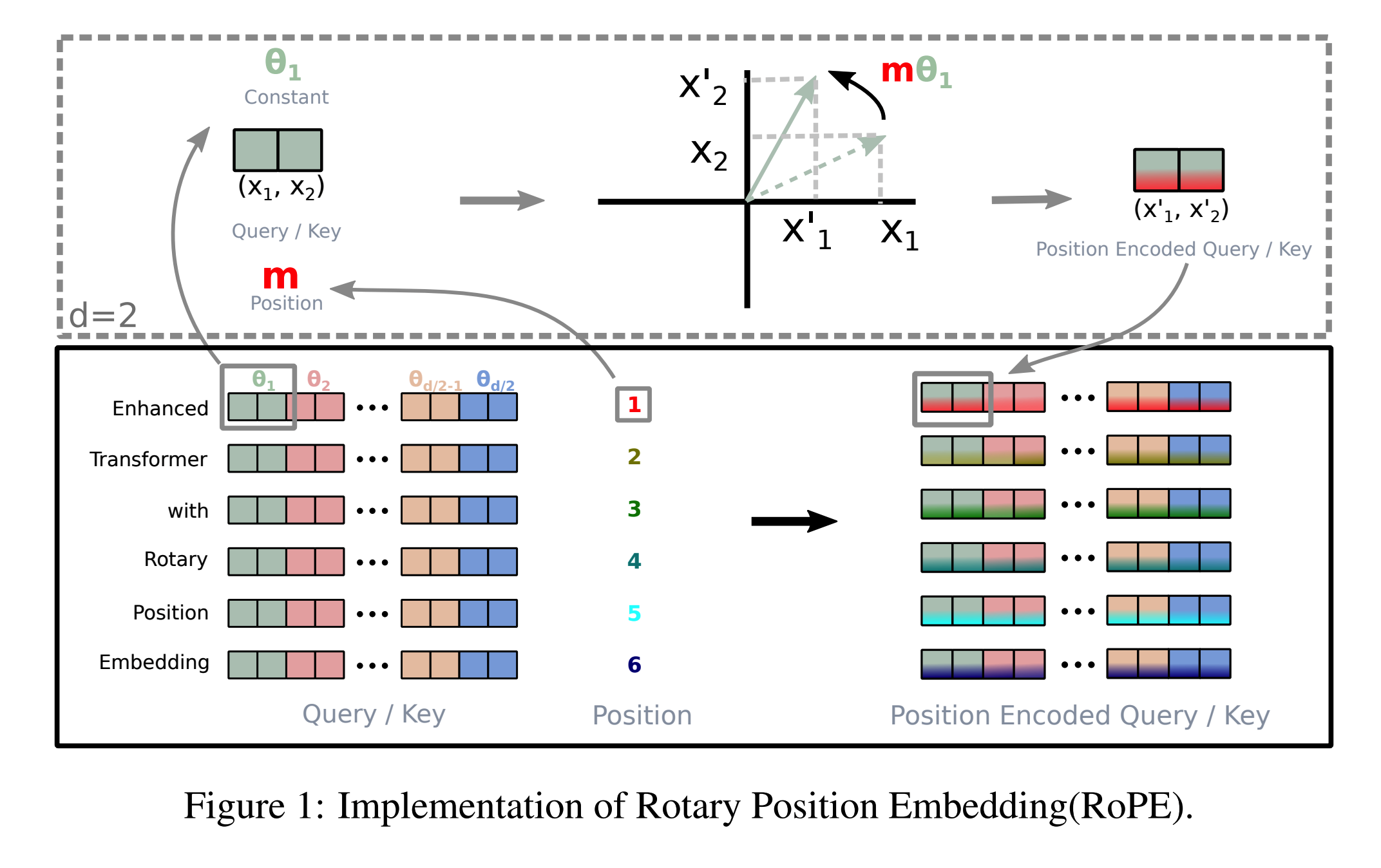
2、线代视角下的数学理解
假设有一段输入中某一个tokens是X,X在注意力机制中有三个向量,分别是Key、Query、Value。
假设 Query 向量的一部分是二维向量:
位置为 p,对应一个旋转角度 θ_p。
通过一个旋转矩阵:
得到位置编码后的
Key向量同理:
他们的注意力机制结果是:
由于旋转矩阵是正交矩阵:
可得:
点积的结果,天然与
3、复数视角下的数学理解
在 RoPE多维推广中,我们总是把相邻两维当成一组:
在复数视角下,它可以自然地表示为一个复数:
同理,Key 的第 i 组:
复数的旋转,则是乘以单位复数;
二维旋转矩阵:
在复数里,对应的操作只需要一行:
也就是说模长 |z| 不变,只改变相位。
在 RoPE 中,位置 p 对应一个角度
于是:
Query 和 Key 的复数表示为:
分别对应第 m的 Query 和第 n 个位置的Key。
二维实向量点积:
这里的实部可以取到
可以看到在复数视角下取共轭,是为了最后可以构造出点积形式,在这里利用复数特性构造共轭复数作为乘数因子:
取实部:
可得到点积(这里的实部为ac+bd,而虚部为bc-ad,正好是叉积式的旋转量)。