RoPE工程视角下的注意力机制流程理解

Author：张一极

2026年01月28日21:42:50

1、概述

本文从工程实现的视角，详细梳理 RoPE 的计算流程，并明确它在 Transformer 架构中带来的具体操作变化。

2、RoPE 在 Attention 机制中的位置

RoPE 与传统的绝对位置编码最大的区别在于插入位置。

• 传统位置编码： 在 Input Embedding 层之后，直接将位置向量加到词向量上： $\mathbf{x}=\text{TokenEmbedding}(x)+\text{PosEmbedding}(pos)$$\mathbf{x} = \text{TokenEmbedding}(x) + \text{PosEmbedding}(pos)$ 然后再输入到 Transformer 层计算。

• RoPE： 不在 Input Embedding 阶段处理，而是在每一层 Transformer 的 Self-Attention 内部进行处理。 具体来说，是在 Query 和 Key 投影之后，Attention Score 计算之前。

几个需要理解的特点：

1. 只旋转 Q 和 K：因为位置信息主要通过 Query 和 Key 的交互（点积）来体现。

2. V 不旋转：Value 向量承载的是内容信息，不需要注入位置偏差。

3. 每一层都做：RoPE 是作用在每一层 Attention 里的，而不是只在第一层。

3、RoPE 计算流程详解

假设我们有一个 Batch 的输入，其中一个序列的长度为 $L$$L$，Embedding 维度为 $D$$D$（这里的 $D$$D$ 通常指 Attention Head 的维度 head_dim）。

对于序列中的第 $m$$m$ 个 token，其 Query 向量为 ${\mathbf{q}}_m$$\mathbf{q}_m$。

a.向量分组

RoPE 的核心是将向量两两配对，在二维平面上旋转。 因此，首先将维度为 $D$$D$ 的向量 ${\mathbf{q}}_m$$\mathbf{q}_m$ 视为 $D/2$$D/2$ 对二维坐标：

分组为：

b.生成旋转频率

我们需要为每一组计算一个特定的旋转角度。 RoPE 定义了一组固定的频率 ${\theta }_i$$\theta_i$，其中 $i$$i$ 是分组索引 ($0,1,...,D/2-1$$0, 1, ..., D/2-1$​)。

通过维度D和位置i，来计算对应位置的旋转角度。

公式为：

• 当 $i=0$$i=0$ (低频分量)时，${\theta }_0=1$$\theta_0 = 1$。

• 当 $i$$i$ 增大 (高频分量)时，${\theta }_i$$\theta_i$​ 迅速减小。

位置i与频率变化如图示：

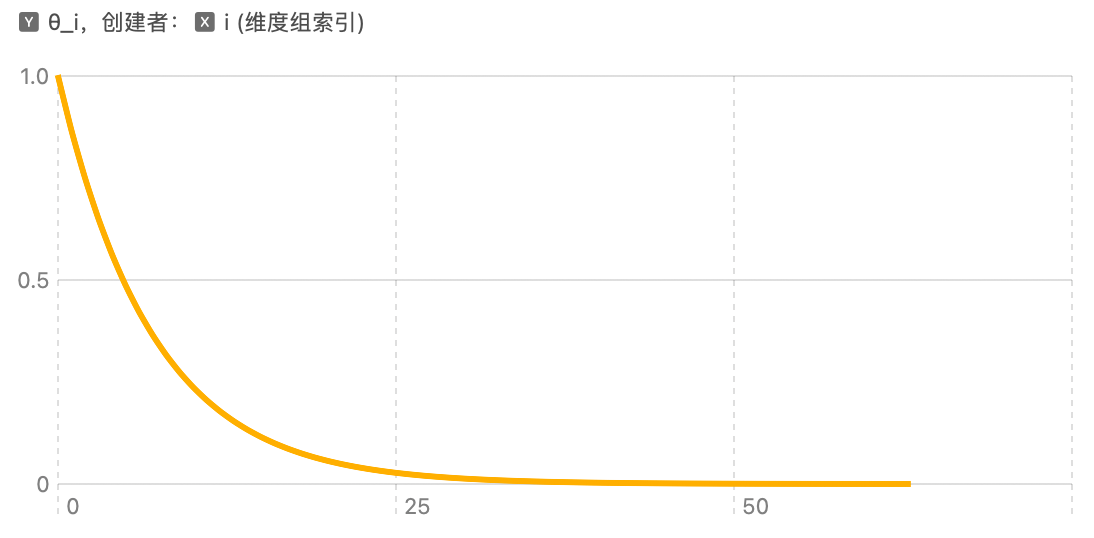
可以看出，随着位置变大，频率迅速衰减。

这意味着：向量的前几维旋转得很快，后几维旋转得很慢。这种多尺度的设计有助于模型同时捕捉长距离和短距离的依赖。

对于位置 $m$$m$，实际的旋转角度是位置乘以频率，这里引入位置的核心原因就是为了最后能够得到$m-n$$m-n$关联位置差：

c.旋转推广

对每一组 $(x,y)$$(x, y)$ 应用旋转矩阵：

展开计算得到：

d.拼接回原形状

原始向量（以 Q 或 K 为例）：

按 2 维一组分成：

对第 i 组做旋转（下标为 2i ）：

拼接结果就是：

即得到 $\text{RoPE}({\mathbf{q}}_m)$$\text{RoPE}(\mathbf{q}_m)$。

4、总结

RoPE 没有引入额外的训练参数（只通过固定的频率*一个已知数），实现了相对位置编码的特性，且兼顾了长短距离上下文的视角。

他的核心流程大概可以总结为：

q和k分别旋转，后面才计算注意力分数。

xxxxxxxxxx
q = apply_rope(q, pos)
k = apply_rope(k, pos)

attn = torch.matmul(q, k.transpose(-2, -1))

以上