极限存在_两个重要极限

高等数学记 📖 极限存在准则

整理：张一极 2020-0321-00:01
个人博客:极度空间
公众号:视觉迷航

第一准则：（夹逼准则）

$n_0$ $n_0$ ,有

1.y_{n} \leqslant x_{n} \leqslant z_{n}

2.\lim _{n \rightarrow \infty} y_{n}=a, \lim _{n \rightarrow \infty} z_{n}=a

两大条件成立，那么xn数列极限存在，并且为a。

推广到函数领域：

g(x) \leqslant f(x) \leqslant h(x) \\ \lim _{x \rightarrow x_{0} \atop(x \rightarrow \infty)} g(x)=A, \lim _{x \rightarrow x_{0} \atop(x \rightarrow \infty)} h(x)=A

接下来书里证明了一个重要的极限：

\lim _{x \rightarrow 0} \frac{\sin x}{x}=1

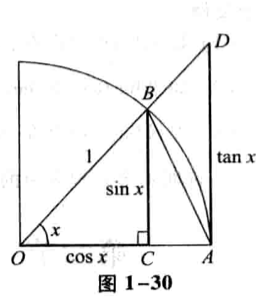
首先，明确两个地方，A是切线，ob是延长线，两者相交于D，BCO是直角三角形，意味着，bco里面，标准的直角三角形，一边为sinx，一边为cosx，剩下的就是tanx：

\sin x=C B, \quad x=A B, \quad \tan x=A D

这里这句话，没必要去懂这个，直接看下一句，aob的小于大于aob扇形，小于三角形aod，故：

\frac{1}{2} \sin x<\frac{1}{2} x<\frac{1}{2} \tan x

为什么呢，因为x限定在了

\angle A O B=x\left(0<x<\frac{\pi}{2}\right)

所以这个式子是一定成立的，我们都知道在四分之一个周期里，这三个函数的排列问题。

如果非得要弄清楚的话，这样解释上面那个不好懂的式子，其实单位圆中，x所对应的角度就是弧度，也就是ab之间的弧度为x，然后同样是斜边为1的直角三角形中，sin = 对边/斜边，所以

\sin x=C B

同理，

\cos x=OC

接着要得到tan，使用sinx/cosx，在大的三角形里，也就是aod里面，tanx = da/oa，oa为r=1：

\tan x=A D

才会有了上面的推论，接着证明的问题转换成了：

\sin x<x<\tan x

两边同时除以sinx，得到：

1<\frac{x}{\sin x}<\frac{1}{\cos x}

进一步转化：

\cos x<\frac{\sin x}{x}<1

或者使用原来的判据，证明1/cos极限为1，原命题即可得证，通过图像可以知道，cos0为1，所以1/cosx，x趋于0的时候，极限为1，原命题得证。

书上的方法是：

用第二个式子：

\cos x<\frac{\sin x}{x}<1

证明cosx趋于1，在x趋于0的时候。

取了一个三角函数变换：

0<|\cos x-1|=1-\cos x=2 \sin ^{2} \frac{x}{2}<2\left(\frac{x}{2}\right)^{2}=\frac{x^{2}}{2}

所以 0<1-\cos x<\frac{x^{2}}{2}

那么x平方趋于0，在x趋于0的时候，故，cosx在x趋于0的时候，极限是1。

根据夹逼定理，得：

\lim _{x \rightarrow 0} \frac{\sin x}{x}=1

通过这个极限，还可以求出，tanx/x的极限：

\lim _{x \rightarrow 0} \frac{\tan x}{x}=\lim _{x \rightarrow 0}\left(\frac{\sin x}{x} \cdot \frac{1}{\cos x}\right)=\lim _{x \rightarrow 0} \frac{\sin x}{x} \cdot \lim _{x \rightarrow 0} \frac{1}{\cos x}=1

夹逼准则应用例题:

$\lim_{x\to 0}x\cdot [\frac{10}{x}]$
其中中括号是取整
解:
$a-1<[a]<=a$
分两种情况讨论 :
$x\to 0^+$
$lim_{x\to 0}x\cdot (\frac{10}{x}-1)<lim_{x\to 0}x\cdot [\frac{10}{x}]<\lim_{x\to 0}x\cdot \frac{10}{x}$
$lim_{x\to 0^+}x\cdot \frac{10}{x}-x=10-x=10$
$lim_{x\to 0^+}x\cdot \frac{10}{x}=10$
$x\to 0^-$
$lim_{x\to 0}x\cdot (\frac{10}{x}-1)>lim_{x\to 0}x\cdot [\frac{10}{x}]>\lim_{x\to 0}x\cdot \frac{10}{x}$
同理可得:
两边的极限依旧为10
故原式极限 = 10

高等数学记 📖 极限存在准则

夹逼准则应用例题:

1.\lim_{x\to 0}x\cdot [\frac{10}{x}]

解:

$\lim_{x\to 0}x\cdot [\frac{10}{x}]$