随机变量的数字特征

Author:张一极
全文5020字,仅供参考
20201128-8:35

期望

同分布样本均值的期望等于总体的期望

离散型随机变量的期望,代表了在这个体系下,会得到一个什么水准的一个数值,使用他的概率,乘以所代表的的值:

E\left(\sum_{i=1}^{n} a_{i} X_{i}\right)=\sum_{i=1}^{n} a_{i} E X_{i}

其对应运算法则如下:

常数:E_{c}=c, ~~一次函数:\quad E(a X+c)=a E X+c, ~~~加减:\quad E(X \pm Y)=E X \pm E Y

方差

样本均值的方差等于总体方差除以n

反映一个数据列的波动情况:

表达方式是用实际情况减去期望,再取平方后的期望均值

D X=E\left[(X-E X)^{2}\right]=E\left(X^{2}\right)-(E X)^{2}

$DX=平方的期望-期望的平方$

$\sqrt {DX}$ 为这个数据列的标准差

一些性质:

\begin{array}{l}D X \geqslant 0\\E\left(X^{2}\right)=D X+(E X)^{2} \geqslant(E X)^{2} \\ D c=0(c \text { 为常数 })\\D(X \pm Y)=D X+D Y \pm 2 \operatorname{Cov}(X, Y) \\ D(a X+b)=a^{2} D X\end{array}

在相互独立的前提下:

D(a X+b Y)=a^{2} D X+b^{2} D Y

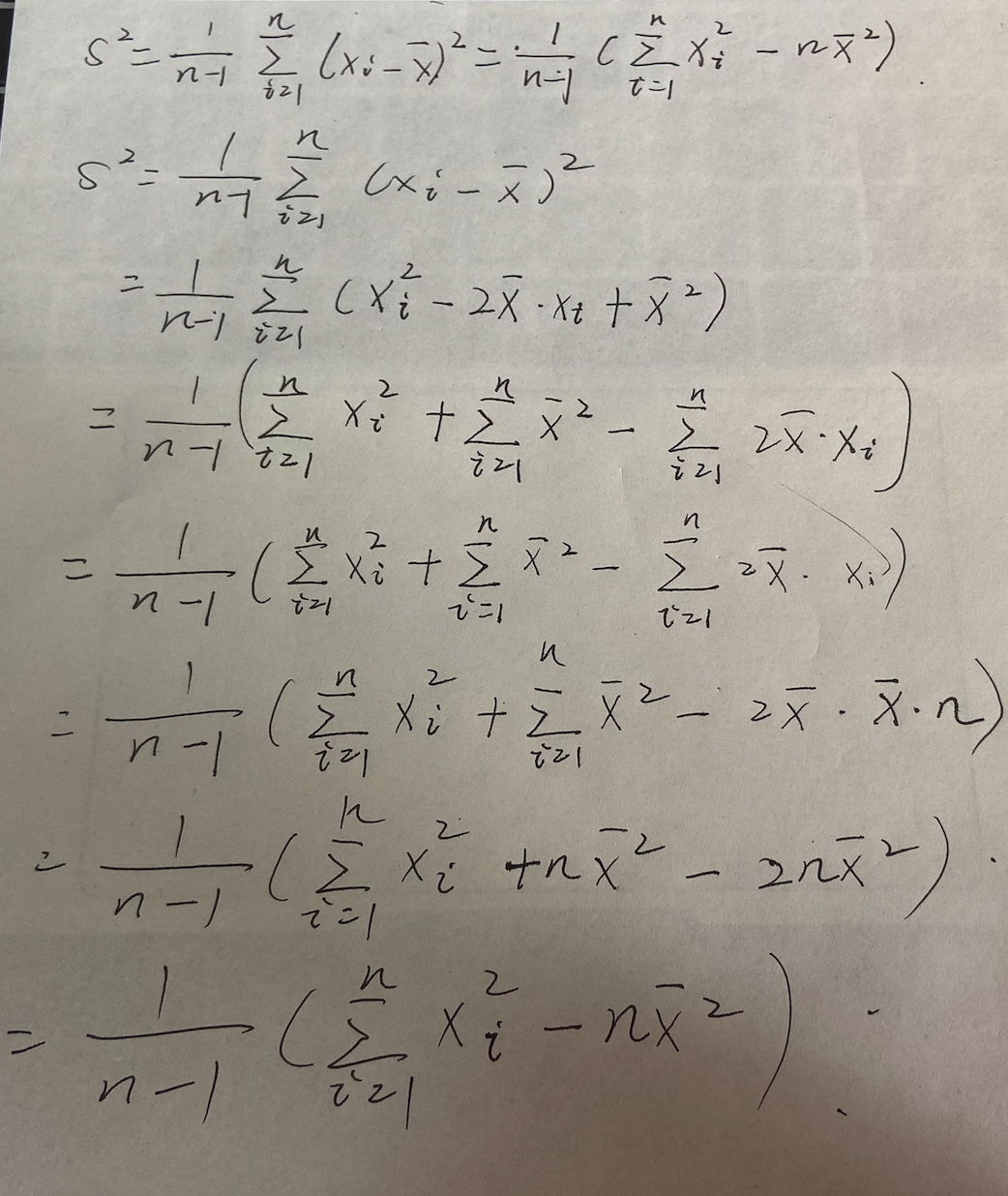
协方差

两个不同的变量之间的波动情况:

\operatorname{Cov}(X, Y)=E[(X-E X)(Y-E Y)]=E(X Y)-E X \cdot E Y

联合期望:

E(X Y)=\left\{\begin{array}{l}\sum_{i} \sum_{j} x_{i} y_{j} P\left\{X=x_{i}, Y=y_{j}\right\}(\text { 离散随机变量 }) \\ \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x y f(x, y) \mathrm{d} x \mathrm{~d} y(\text { 连续随机变量}) .\end{array}\right.

切比雪夫不等式的两种情况:

关于证明：
本证明只是一个不严谨版本的证明，为帮助串联起概率密度函数和期望的定义等一系列知识点，所作总结
证明如下：
假定X服从于某个分布，依据我们所达成的共识，即其概率值大于0
$\mathrm{P}(X \geq a) \leq \frac{\mathrm{E}(X)}{a}$ ，如果要证明切比雪夫，我们先来看Markov不等式的证明，我们知道一个随机变量X大于或者小于某个值的概率，就是对概率密度函数在相应范围内做积分，客观上，我们对整个定义域（正无穷到负无穷）做积分，得到的就是1，即这个随机变量的所有事件发生的概率值之和，一定为1，接着我们需要知道期望的定义：
1.离散条件下，就是X乘以其对应概率的和
$xf(x)$ ，即：

$\mathrm{E}(X)=\int_{-\infty}^{\infty} x f(x) d x$
$E（x）=\int_{0}^{\infty} x f(x) d x$
那么现在，我们暂且假设概率密度函数图像如下：
$p_1$ $p_2$ $p_1>p_2$ (绿色覆盖面积较大，覆盖到的概率密度越大，代表的其概率更大，这是概率密度函数的特点)，所以期望也一定较大。
所以一定有：
$\begin{aligned} \mathrm{E}(X) &=\int_{-\infty}^{\infty} x f(x) d x \\ &=\int_{0}^{\infty} x f(x) d x \\ & \geqslant \int_{a}^{\infty} x f(x) d x \\\because 证明的是X>=a的概率,\therefore & \geqslant \int_{a}^{\infty} a f(x) d x \\ &=a \int_{a}^{\infty} f(x) d x ~~(a当做常数提出即可)\end{aligned}$
$\mathrm{P}(X \geq a) \leq \frac{\mathrm{E}(X)}{a}$ $|X-\mu|$ $P(|X-\mu|>a) \leq \frac{E(|X-\mu|)}{a}$ $P\left((X-\mu)^{2} \geq a^{2}\right) \leq \frac{E\left((X-\mu)^{2}\right)}{a^{2}}$
$E(X-\mu)^{2}=E（X^2-2\mu\cdot \mu+\mu^2）=E(X^2)-2E(X)^2+E(X)^2=E(X^2)-E(X)^2=D(X)=\sigma^2$ ,即得到：
$P\left((X-\mu)^{2} \geq a^{2}\right) \leq \frac{E\left((X-\mu)^{2}\right)}{a^{2}}=\frac{\sigma^{2}}{a^{2}}$
$\varepsilon$ ，即得到下式，至此，证毕。

P\left\{|X-E X| \geqslant_{\varepsilon}\right\} \leqslant \frac{D X}{\varepsilon^{2}}

P\{|X-E X|<\varepsilon\} \geqslant 1-\frac{D X}{\varepsilon^{2}}

二维正态分布

参数:

(X, Y) \sim N\left(\mu_{1}, \mu_{2}, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)

参数范围:

\mu_{1}, \mu_{2}, \sigma_{1}>0, \sigma_{2}>0,|\rho|<1

密度函数:

f(x,y)=\frac{1}{2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}} e^{-\frac{1}{2\left(1-\rho^{2}\right)}}\left[\left(\frac{x-\mu_{1}}{\sigma_{1}}\right)^{2}-\frac{2 \rho\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1} \sigma_{2}}+\left(\frac{y-\mu_{2}}{\sigma_{2}}\right)^{2}\right]

参数意义:

\mu_{1}=E X, \mu_{2}=E Y, \sigma_{1}^{2}=D X ; \sigma_{2}^{2}=D Y

这两个子分布依然是正态分布:

X \sim N\left(\mu_{1}, \sigma_{1}^{2}\right), Y \sim N\left(\mu_{2,} \sigma_{2}^{2}\right)

$X_{new}$ $Y_{new}$ $X \sim N\left(\mu_{1}, \sigma_{1}^{2}\right), Y \sim N\left(\mu_{2}, \sigma_{2}^{2}\right)$ ,其联合分布,未必是正态分布

$\rho=0$

$a \mathbf{X}+\mathrm{b} \mathrm{Y} \sim \mathrm{N}\left(\mathrm{a} \mu_{1}+\mathrm{b} \mu_{2}, \mathrm{a}^{2} \sigma_{1}^{2}+\right.\left.\mathrm{b}^{2} \sigma_{2}^{2}+2 \mathrm{ab} \rho \sigma_{1} \sigma_{2}\right)$

$\bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}$ 服从（0，1/n）的正态分布

依概率收敛

$\varepsilon>0$ , Y是一个随机变量序列,a是一个常数,一个随机变量序列和一个常数的差小于某个大于0的数,在随着序列不断增长其差小于这个数的概率越发趋近于1的情况

\lim _{n \rightarrow \infty} P\left\{\left|Y_{n}-a\right| \leq \varepsilon\right\}=1

$Y_{n} \stackrel{P}{\rightarrow} a$ .

切比雪夫大数定律

$X_{1}, X_{2}, \cdots, X_{n}, \cdots$ $E\left[X_{n}\right]=\mu, D\left[X_{n}\right]=\sigma^{2}$ $\bar{X}=\frac{1}{n} \sum_{k=1}^{n} X_{k}$ $\mu$ .

主要应用形式：

P(|X-E（X）| \geq \varepsilon) \leq \frac{V a r X}{\varepsilon^{2}}

一.相互独立
二.方差有界

伯努利大数定律

一个n重独立重复实验中,事件发生的频率逼近其概率,其数学描述:

$n_1$ $p$ $\lim _{n \rightarrow \infty} P\left\{\left|\frac{n_{1}}{n}-p\right|<\varepsilon\right\}=1$

辛钦定理

$\mu$ $\varepsilon$ $\lim _{n \rightarrow \infty} P\left\{\left|\frac{1}{n} \sum_{k=1}^{n} X_{k}-\mu\right|<\varepsilon\right\}=1$

不难看出,如果每个事件概率相同,则变成了伯努利大数定律的场景,所以我们知道,伯努利大数定律是辛钦定理的一个特殊情况(n重独立实验)

一.独立
二.同分布
三.期望存在

中心极限定理

列-林德伯格定理

中心极限定理阐述了一件事情:

$X_{1}, X_{2}, \cdots, X_{n}X_{1}, X_{2}, \cdots, X_{n}$ $\mathbb{E}\left[X_{k}\right]=\mu, \operatorname{Var}\left[X_{k}\right]=\sigma^{2}$ $\overline {SumX_n}$ $\overline {SumXn}$ $(n\mu,n\sigma^2)$ $\frac{\overline{S X_{n}}-n \mu}{\sqrt{n} \sigma}$ $N(0,1)$

$\mu, \sigma^{2}$ $X_{1}, X_{2}, \cdots, X_{n}$ $\overline{S X_{n}}=\sum_{k=1}^{n} X_{k}$ $N\left(n \mu, n \sigma^{2}\right)$

Demoiver-Laplace定理

$\lim _{n \rightarrow \infty} P\left\{\frac{\eta_{n}-n p}{\sqrt{n p(1-p)}} \leq x\right\}=\int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} e^{-t^{2} \mid 2} d t=\Phi(x)$ 正态分布是二项分布的极限分布。当n充分大时，可以利用正态分布来计算二项分布的概率。

Reference :
[1] http://www.huaxiaozhuan.com/数学基础/chapters/2_probability.html
[2] https://zh.wikipedia.org/wiki/正态分布
[3] https://www.shuxuele.com/data/standard-normal-distribution.html

20:37-20201128
晚安~