Efficientnet解读
Author:张一极
efficientnet致力于寻找一个方法,去平衡flops和一些sota结果的网络架构之间的关系,首先给出了影响网络效率的几个参数,图像的尺寸,网络深度,网络的广度,面临的问题就是过于深入的网络,会造成梯度弥散等问题,精度不增反降,引出了resnet的发明,而后成为了imagenet的冠军之作,在这里:
ResNet (He et al., 2016) can be scaled up from ResNet-18 to ResNet-200 by using more layers; Recently, GPipe (Huang et al., 2018) achieved 84.3% Ima- geNet top-1 accuracy by scaling up a baseline model
指出了resnet的基本backone之上,进行网络的scale,微调过后,加深网络深度,获取更好的top1和top5精度.
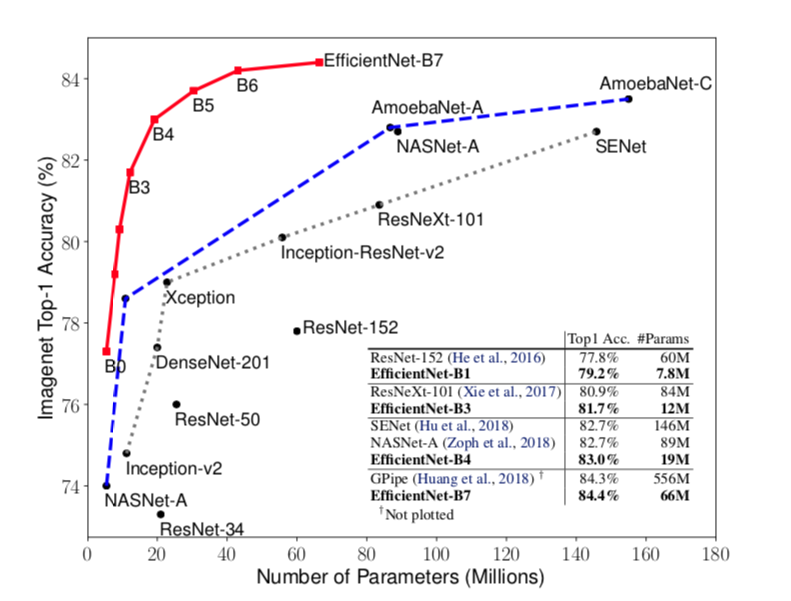
在这张图像里面可以看出,单看精度和flops,Efficientnet精度优于最好的网络,并且在参数量方面也有很大的优势.
In particular, EfficientNet-B7 achieves new state-of-the-art 84.4% top-1 accuracy but being 8.4x smaller and 6.1x faster than GPipe. EfficientNet-B1 is 7.6x smaller and 5.7x faster than ResNet-152.
单纯的尺寸优势不能够带来其他方面的提高,下图体现了单一维度的网络架构scale
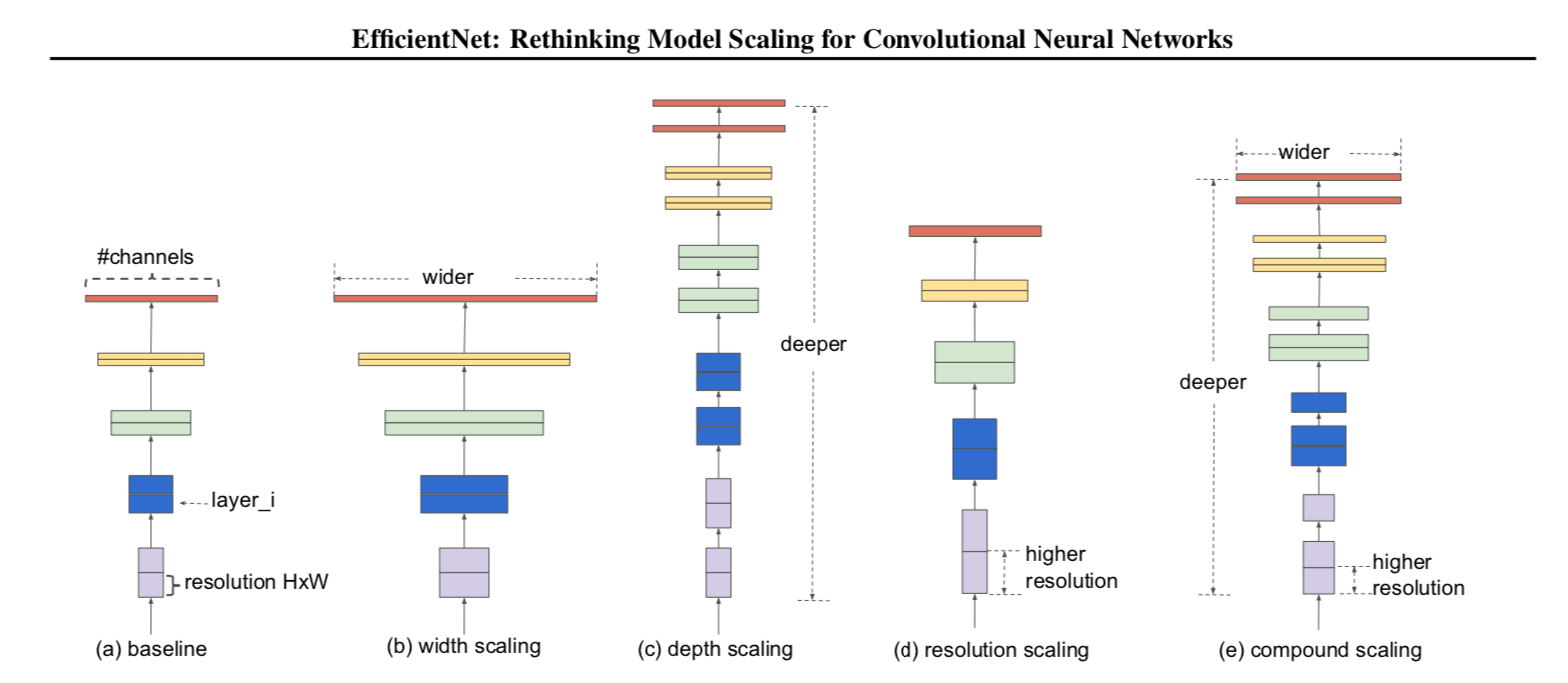
(a) is a baseline network example; (b)-(d) are conventional scaling that only increases one dimension of network width, depth, or resolution. (e) is our proposed compound scaling method that uniformly scales all three dimensions with a fixed ratio.
a是基准网络
b-d是不同尺度的拉伸后的网络
e是通过自适应尺度拉伸的网络
使用三个系数规划这三个维度的缩放
then we can simply increase the network depth by αN, width by βN, and image size by γN, where α,β,γ are constant coefficients determined by a small grid search on the original small model.
在大尺寸的图像里面,必须采用多通道去提取图像信息,也可以采用更深的网络架构,去获取更好的图像信息,论文示范了如何使用规模缩放,使用规则,在实验中发现,规则缩放,很依赖于一个好的基准网络,论文使用了一个通过nas搜索得到的网络结构,改变他的尺寸,获取到了一个网络系列,就是论文的efficientnet,
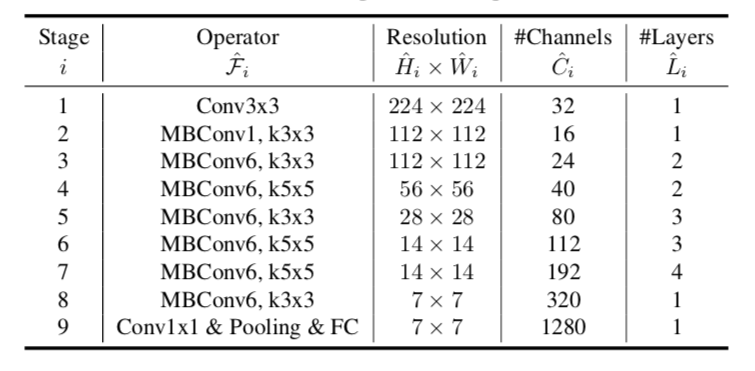
这里的表达了每一次重复计算在每一个步骤里面,而efficientnet在不改变原有网络结构的前提下,去自动适应获取最好效果的网络宽度广度和深度,目标是拿到最好效果和最优参数的结构网络.
预定义好一些参数的basemodel:
在微调网络的过程中,我们知道,更深的网络可以捕获更多的图像信息,还有更完整的图像特征,生成更好的feature map,在新的任务上面,然而,太深的网络是很难训练下去的,会面临梯度消失的问题,于是我们使用跳层链接(resnet)和批量归一化等一系列操作,更宽的网络可以获得更好的纹理特征,并且使得网络更易于训练,但是他很难获取到更高维度的图像特征,在下图左边的实验结果中可以看出,更宽的网络更容易使得测试精度趋于饱和,更大的图像输入,可以让网络获得更好的纹理信息和特征,从224*224到299再到331的图像输入,稳步获取了更好的精度,而最近的工作GPipe获取了一个sota的结果,他的网络输入是480,下图右边体现了尺度变化给网络精度带来的变化.
右图 r = 1.0 denotes resolution 224x224 and r = 2.5 denotes resolution 560x560
ResNet-1000 has similar accuracy as ResNet-101 even though it has much more layers. Figure 3 (middle) shows our empirical study on scaling a baseline model with different depth coefficient d, further suggesting the diminishing accuracy return for very deep ConvNets.
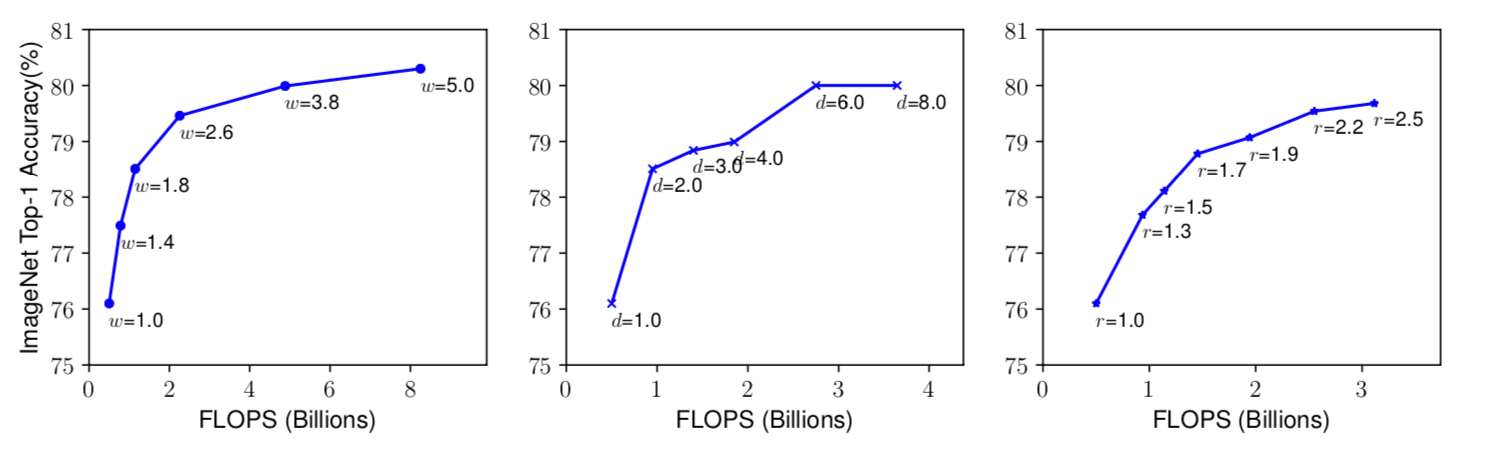
第一张图像表示了网络宽度带来的精度改变 , 第二张图表示了网络深度带来的改变 ,第三张图表示了输入图像的分辨率带来的精度改变,可以发现的是,最后达到了80%左右精度就很难获得很大的提高了.
可以得到的结论就是,更大的网络宽度,深度和图像输入尺寸可以获取更高的精度,但是在最后,精度上涨十分有限.于是实验人员做了下一步观测,不同尺度系数之间进行尺度变化,效果如下:
If we only scale network width w without changing depth (d=1.0) and resolution (r=1.0), the accuracy saturates quickly. With deeper (d=2.0) and higher resolution (r=2.0), width scaling achieves much better accuracy under the same FLOPS cost. These results lead us to the second observation:
引出第二个观测:
首先怼了一下目前的一些工作,手动调参没什么意义,针对任务去调:
In fact, a few prior work (Zoph et al., 2018; Real et al., 2019) have already tried to arbitrarily balance network width and depth, but they all require tedious manual tuning.
提出了一个混合调节方法:
其中Aloha和Gama还有Bata是一个常量,可以通过一个小型的网格搜索获取到,
是一个具体的系数,来规范模型资源用量的值,在本paper中:
In this paper, we constraint α · β2 · γ2 ≈ 2 such that for any new φ, the total FLOPS will approximately3 increase by 2φ.
在basemodel选择方面,研究并不选择现有的网络,为了更好的示范效果,研究选择了一个搜索出来的网络作为basemodel.
ACC(m)×[FLOPS(m)/T]w as the optimization goal, where ACC(m) and FLOPS(m) denote the accu- racy and FLOPS of model m
使用acc和flops作为更好的一个优化指标,通过搜索basemodel
获得b0-b7
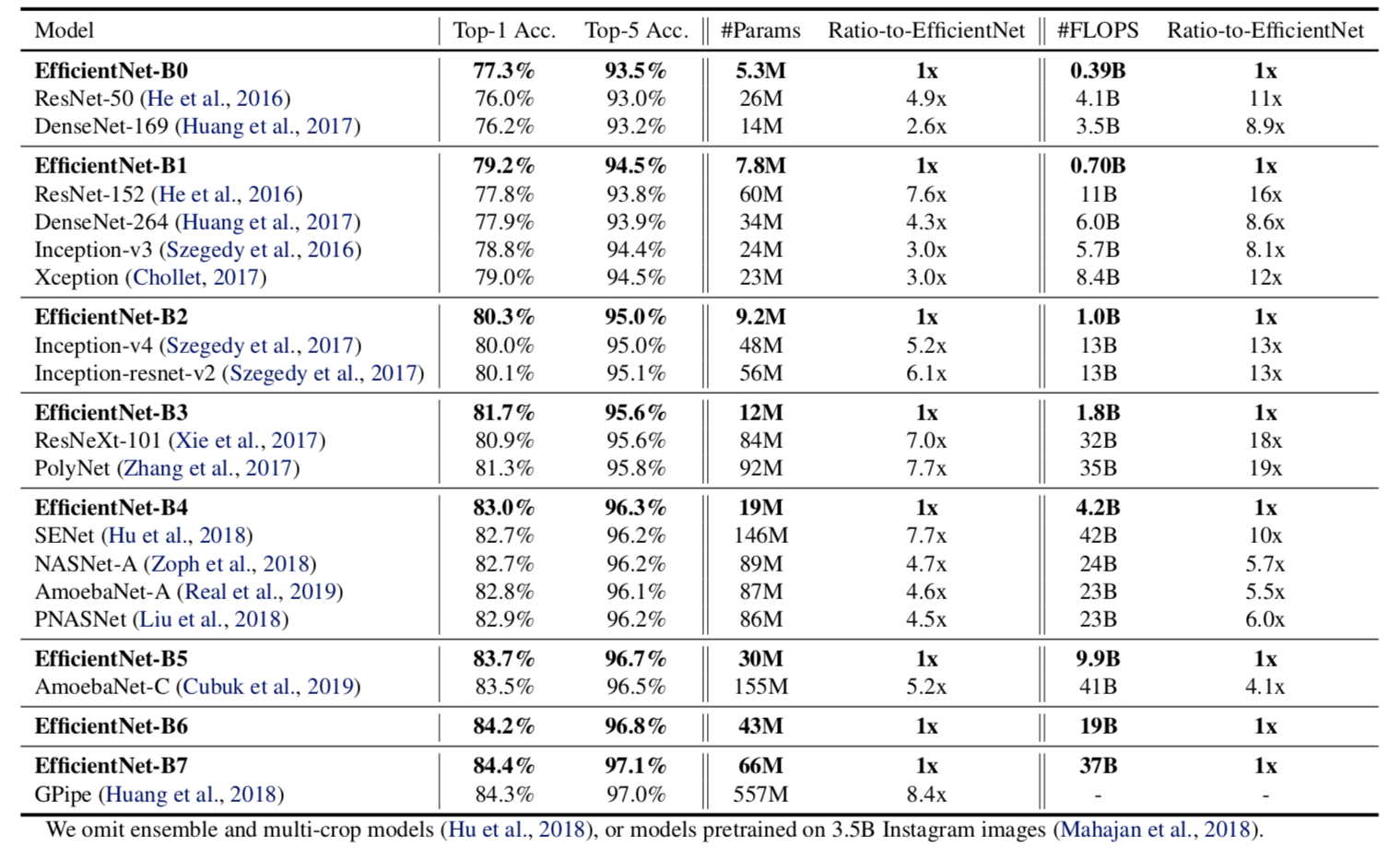
All EfficientNet models are scaled from our baseline EfficientNet-B0 using different compound coefficient φ in Equation 3. ConvNets with similar top-1/top-5 accuracy are grouped together for efficiency comparison. Our scaled EfficientNet models consistently reduce parameters and FLOPS by an order of magnitude (up to 8.4x parameter reduction and up to 16x FLOPS reduction) than existing ConvNets.
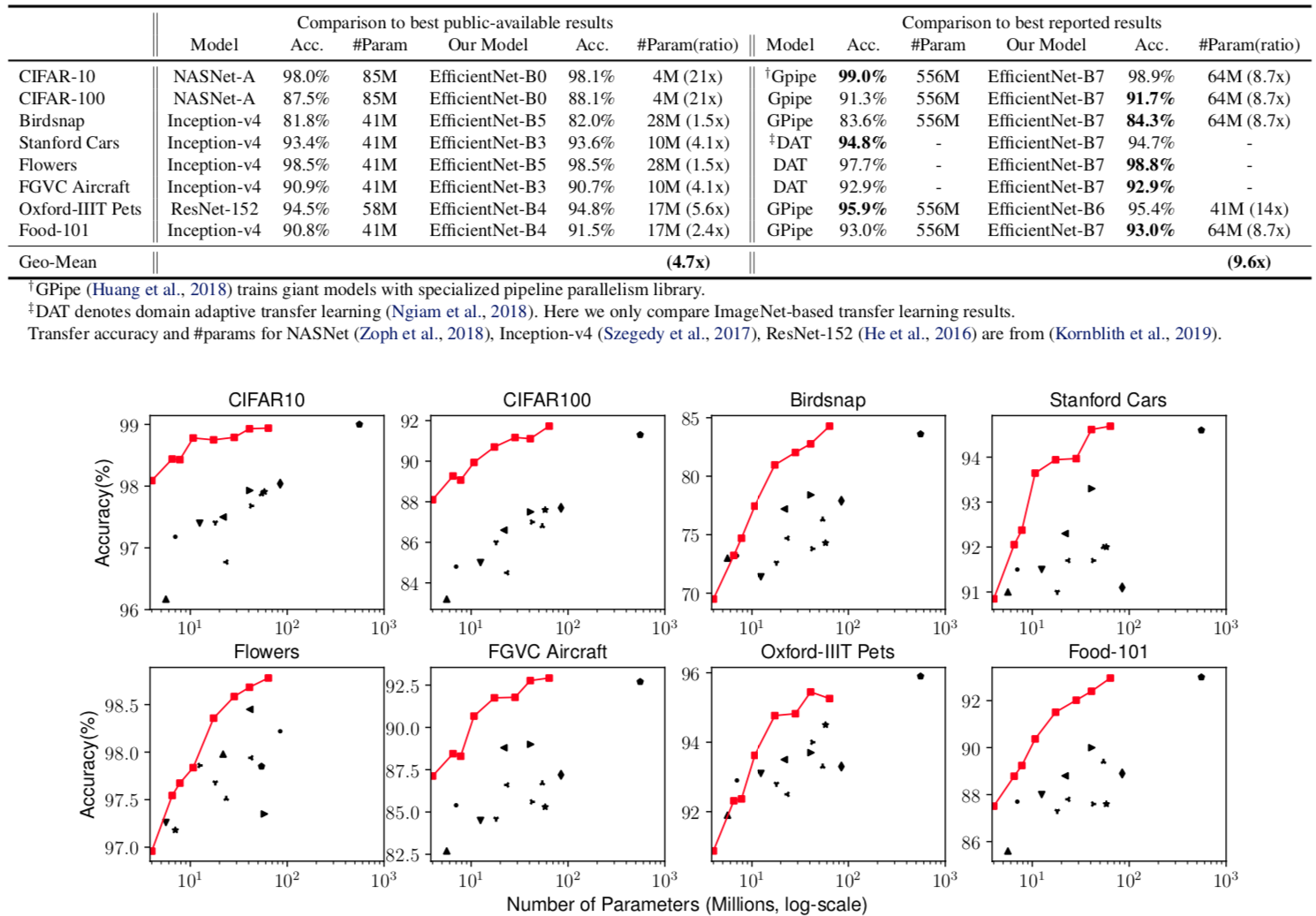
具体的结果,不再赘述了哈.
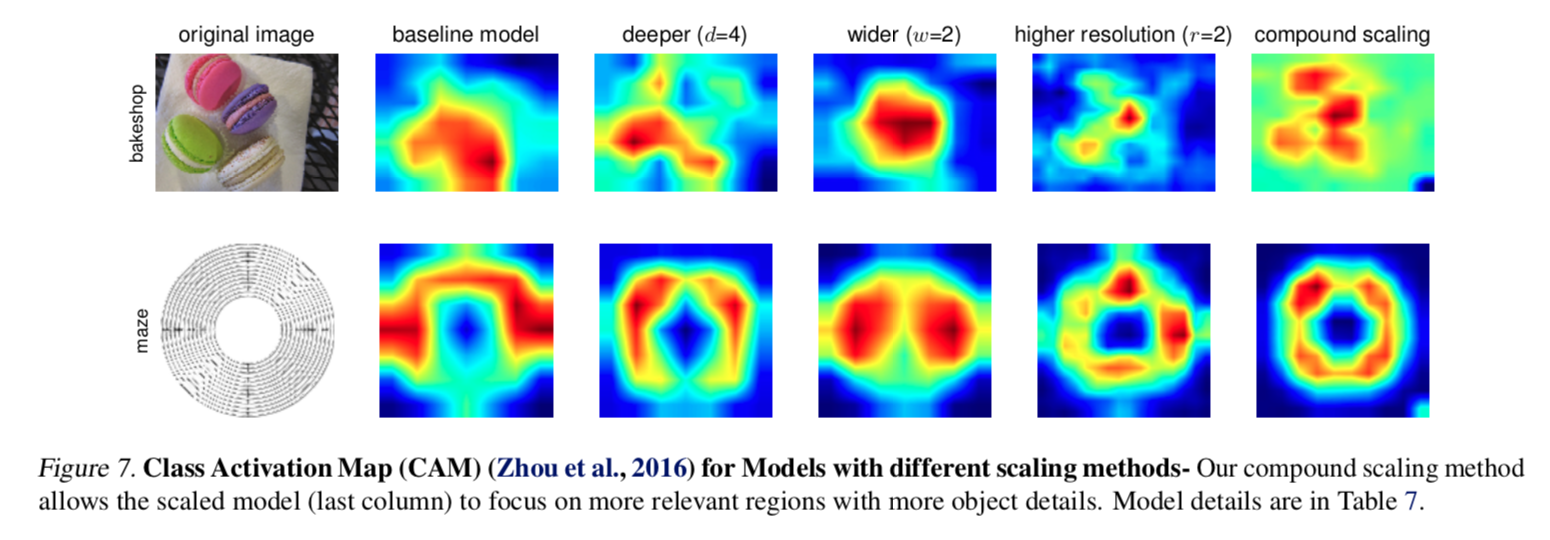
值得一提的是,研究在最后还做了一个cam算法激活,对于模型的注意力去验证,说明经过规范调节的模型,确实把更多的注意力放在物体本身.
论文地址: